ARIMA

An introduction to ARIMA forecasting with scalecast.

[1]:

import pandas as pd
import numpy as np
from scalecast.Forecaster import Forecaster
from scalecast.auxmodels import auto_arima
import matplotlib.pyplot as plt
import seaborn as sns
import warnings

[2]:

df = pd.read_csv('AirPassengers.csv')
f = Forecaster(
    y=df['#Passengers'],
    current_dates=df['Month'],
    future_dates = 12,
    test_length = .2,
    cis = True,
)
f

[2]:

Forecaster(
    DateStartActuals=1949-01-01T00:00:00.000000000
    DateEndActuals=1960-12-01T00:00:00.000000000
    Freq=MS
    N_actuals=144
    ForecastLength=12
    Xvars=[]
    TestLength=28
    ValidationMetric=rmse
    ForecastsEvaluated=[]
    CILevel=0.95
    CurrentEstimator=mlr
    GridsFile=Grids
)

Naive Simple Approach

  • this is not meant to be a demonstration of a model that is expected to be accurate

  • it is meant to show the mechanics of using scalecast

[3]:

f.set_estimator('arima')
f.manual_forecast(call_me='arima1')

[4]:

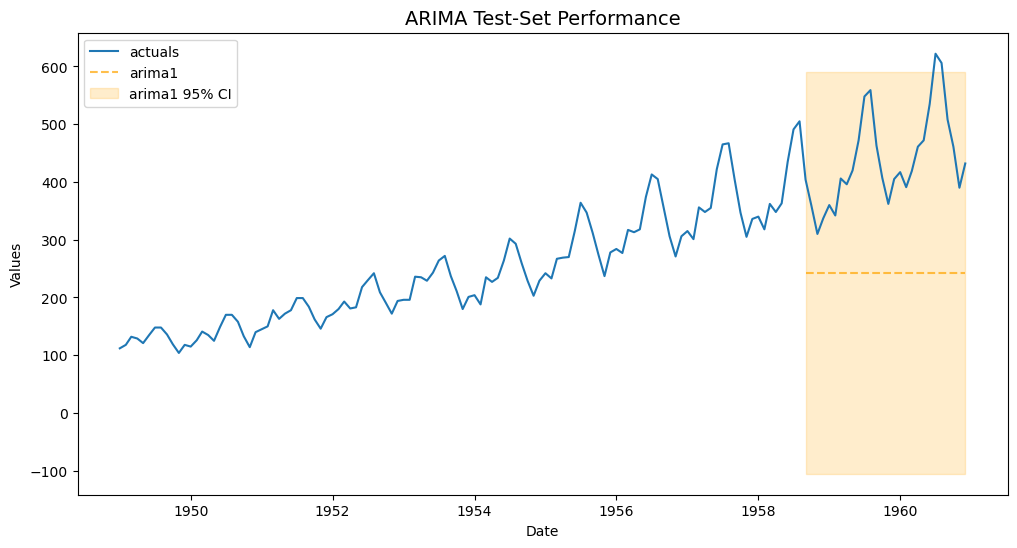
f.plot_test_set(ci=True)
plt.title('ARIMA Test-Set Performance',size=14)
plt.show()
../_images/arima_arima_5_0.png 
[5]:

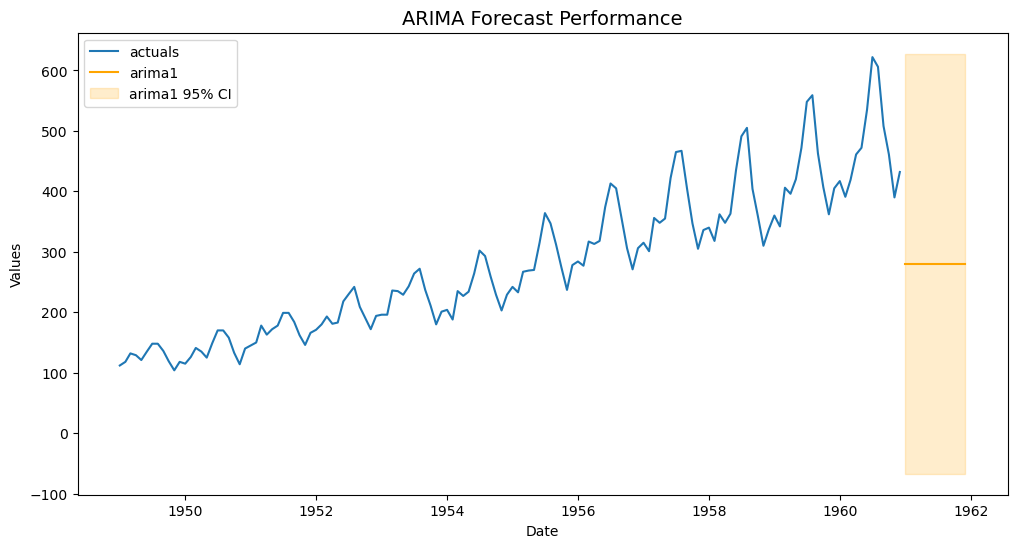
f.plot(ci=True)
plt.title('ARIMA Forecast Performance',size=14)
plt.show()
../_images/arima_arima_6_0.png

Human Interpretation Iterative Approach

  • this is a non-automated approach to ARIMA forecasting where model specification depends on human-interpretation of statistical results and charts

[6]:

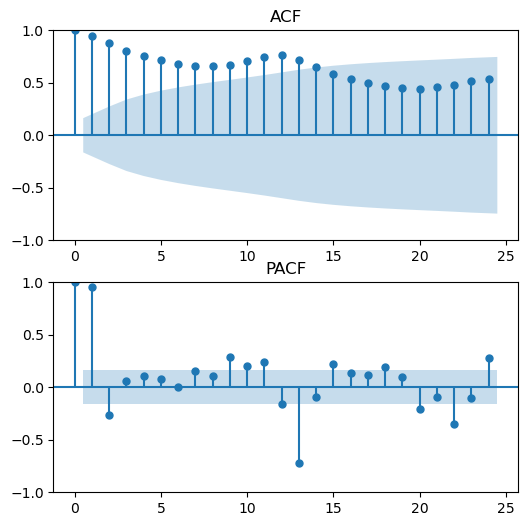
figs, axs = plt.subplots(2, 1,figsize=(6,6))
f.plot_acf(ax=axs[0],title='ACF',lags=24)
f.plot_pacf(ax=axs[1],title='PACF',lags=24)
plt.show()

/Users/uger7/opt/anaconda3/envs/scalecast-env/lib/python3.8/site-packages/statsmodels/graphics/tsaplots.py:348: FutureWarning: The default method 'yw' can produce PACF values outside of the [-1,1] interval. After 0.13, the default will change tounadjusted Yule-Walker ('ywm'). You can use this method now by setting method='ywm'.
  warnings.warn(
../_images/arima_arima_8_1.png 
[7]:

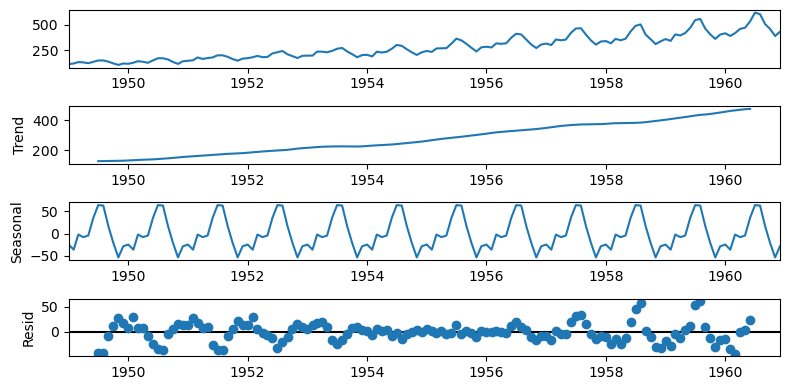
plt.rc("figure",figsize=(8,4))
f.seasonal_decompose().plot()
plt.show()
../_images/arima_arima_9_0.png 
[8]:

stat, pval, _, _, _, _ = f.adf_test(full_res=True)
print(stat)
print(pval)

0.8153688792060442
0.9918802434376409

[9]:

f.manual_forecast(order=(1,1,1),seasonal_order=(2,1,1,12),call_me='arima2')

[10]:

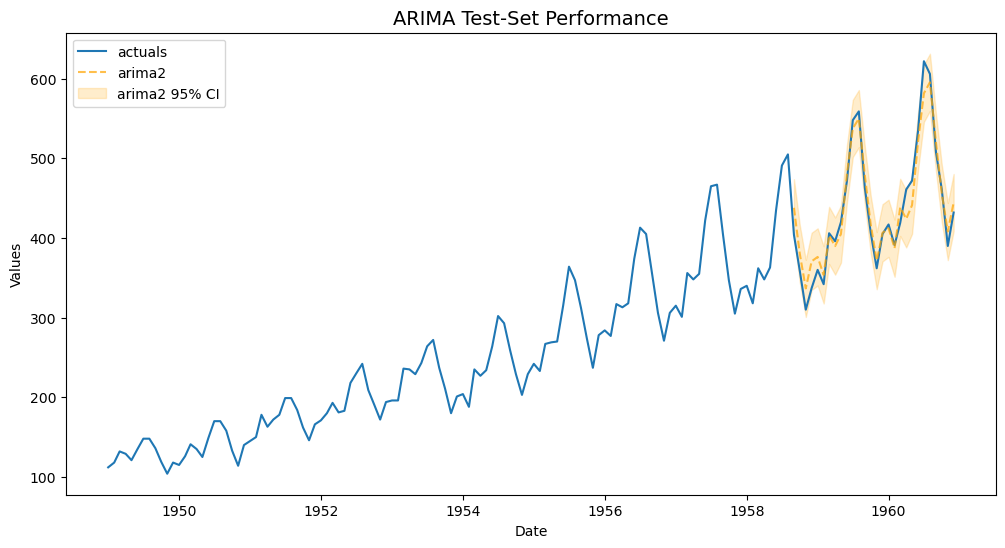
f.plot_test_set(ci=True,models='arima2')
plt.title('ARIMA Test-Set Performance',size=14)
plt.show()
../_images/arima_arima_12_0.png 
[11]:

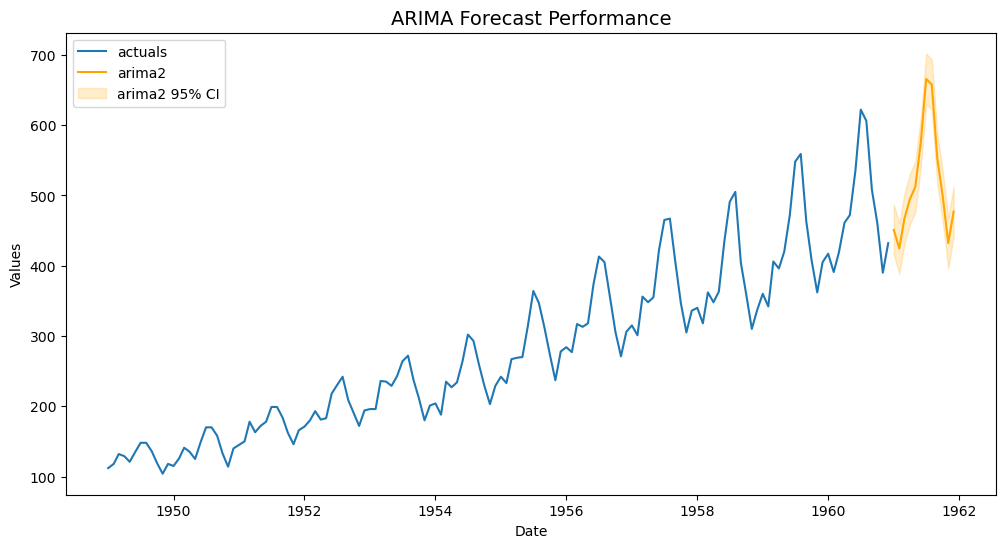
f.plot(ci=True,models='arima2')
plt.title('ARIMA Forecast Performance',size=14)
plt.show()
../_images/arima_arima_13_0.png 
[12]:

f.regr.summary()

[12]:
SARIMAX Results
Dep. Variable: y No. Observations: 144
Model: ARIMA(1, 1, 1)x(2, 1, 1, 12) Log Likelihood -501.929
Date: Mon, 10 Apr 2023 AIC 1015.858
Time: 18:47:23 BIC 1033.109
Sample: 0 HQIC 1022.868
- 144
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 -0.0731 0.273 -0.268 0.789 -0.608 0.462
ma.L1 -0.3572 0.249 -1.436 0.151 -0.845 0.130
ar.S.L12 0.6673 0.160 4.182 0.000 0.355 0.980
ar.S.L24 0.3308 0.099 3.341 0.001 0.137 0.525
ma.S.L12 -0.9711 1.086 -0.895 0.371 -3.099 1.157
sigma2 111.1028 98.277 1.131 0.258 -81.517 303.722
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 7.72
Prob(Q): 0.99 Prob(JB): 0.02
Heteroskedasticity (H): 2.77 Skew: 0.08
Prob(H) (two-sided): 0.00 Kurtosis: 4.18


Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

Auto-ARIMA Approach

pip install pmdarima

[13]:

auto_arima(
    f,
    m=12,
    call_me='arima3',
)

[14]:

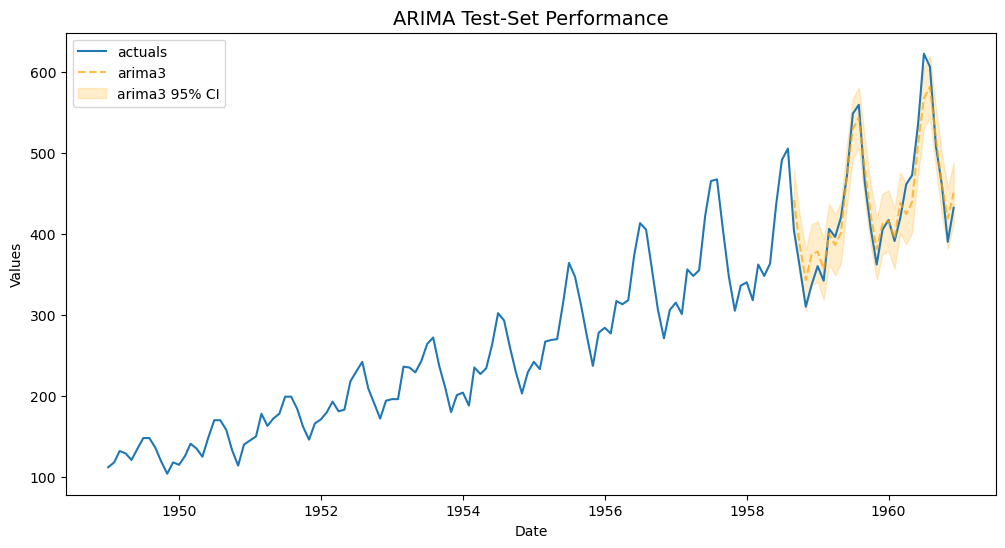
f.plot_test_set(ci=True,models='arima3')
plt.title('ARIMA Test-Set Performance',size=14)
plt.show()
../_images/arima_arima_17_0.png 
[15]:

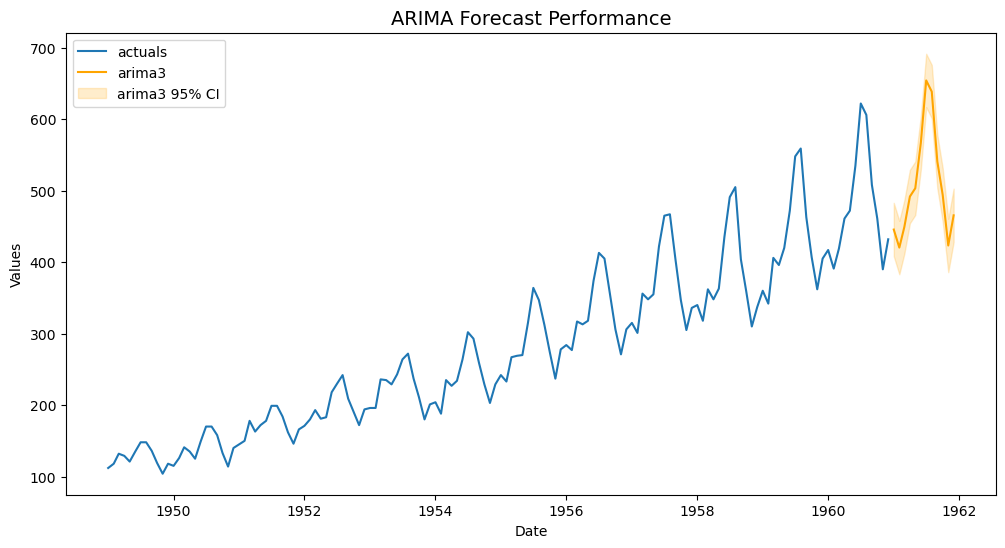
f.plot(ci=True,models='arima3')
plt.title('ARIMA Forecast Performance',size=14)
plt.show()
../_images/arima_arima_18_0.png 
[16]:

f.regr.summary()

[16]:
SARIMAX Results
Dep. Variable: y No. Observations: 144
Model: ARIMA(2, 1, 1)x(0, 1, [], 12) Log Likelihood -504.923
Date: Mon, 10 Apr 2023 AIC 1017.847
Time: 18:47:55 BIC 1029.348
Sample: 0 HQIC 1022.520
- 144
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 0.5960 0.085 6.986 0.000 0.429 0.763
ar.L2 0.2143 0.091 2.343 0.019 0.035 0.394
ma.L1 -0.9819 0.038 -25.599 0.000 -1.057 -0.907
sigma2 129.3177 14.557 8.883 0.000 100.786 157.850
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 7.68
Prob(Q): 0.98 Prob(JB): 0.02
Heteroskedasticity (H): 2.33 Skew: -0.01
Prob(H) (two-sided): 0.01 Kurtosis: 4.19


Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

Grid Search Approach

[17]:

f.set_validation_length(12)
grid = {
    'order':[
        (1,1,1),
        (1,1,0),
        (0,1,1),
    ],
    'seasonal_order':[
        (2,1,1,12),
        (1,1,1,12),
        (2,1,0,12),
        (0,1,0,12),
    ],
}

f.ingest_grid(grid)
f.tune()
f.auto_forecast(call_me='arima4')

[18]:

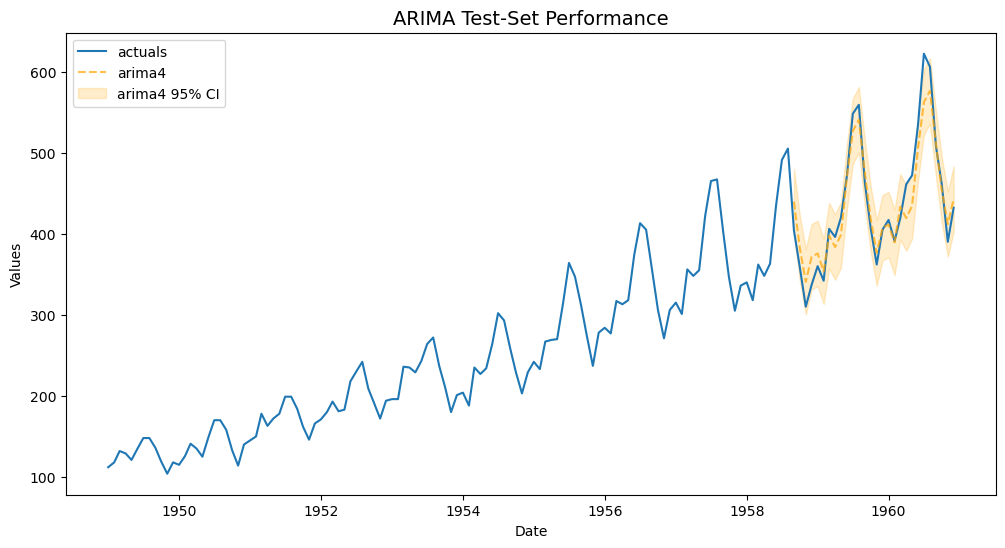
f.plot_test_set(ci=True,models='arima4')
plt.title('ARIMA Test-Set Performance',size=14)
plt.show()
../_images/arima_arima_22_0.png 
[19]:

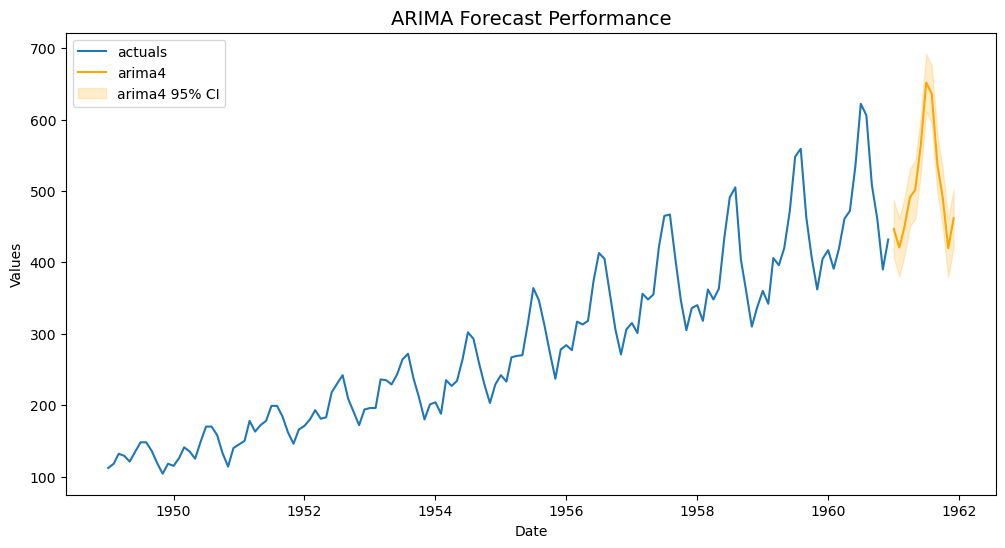
f.plot(ci=True,models='arima4')
plt.title('ARIMA Forecast Performance',size=14)
plt.show()
../_images/arima_arima_23_0.png 
[20]:

f.regr.summary()

[20]:
SARIMAX Results
Dep. Variable: y No. Observations: 144
Model: ARIMA(0, 1, 1)x(0, 1, [], 12) Log Likelihood -508.319
Date: Mon, 10 Apr 2023 AIC 1020.639
Time: 18:50:43 BIC 1026.389
Sample: 0 HQIC 1022.975
- 144
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ma.L1 -0.3184 0.063 -5.038 0.000 -0.442 -0.195
sigma2 137.2653 15.024 9.136 0.000 107.818 166.713
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 5.46
Prob(Q): 0.95 Prob(JB): 0.07
Heteroskedasticity (H): 2.37 Skew: 0.02
Prob(H) (two-sided): 0.01 Kurtosis: 4.00


Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

Export Results

[21]:

pd.options.display.max_colwidth = 100
results = f.export(to_excel=True,excel_name='arima_results.xlsx',determine_best_by='TestSetMAPE')
summaries = results['model_summaries']
summaries[['ModelNickname','HyperParams','InSampleMAPE','TestSetMAPE']]

[21]:
ModelNickname HyperParams InSampleMAPE TestSetMAPE
0 arima2 {'order': (1, 1, 1), 'seasonal_order': (2, 1, 1, 12)} 0.044448 0.037170
1 arima4 {'order': (0, 1, 1), 'seasonal_order': (0, 1, 0, 12)} 0.046529 0.044054
2 arima3 {'order': (2, 1, 1), 'seasonal_order': (0, 1, 0, 12), 'trend': None} 0.045081 0.045936
3 arima1 {} 0.442457 0.430066 
[22]:

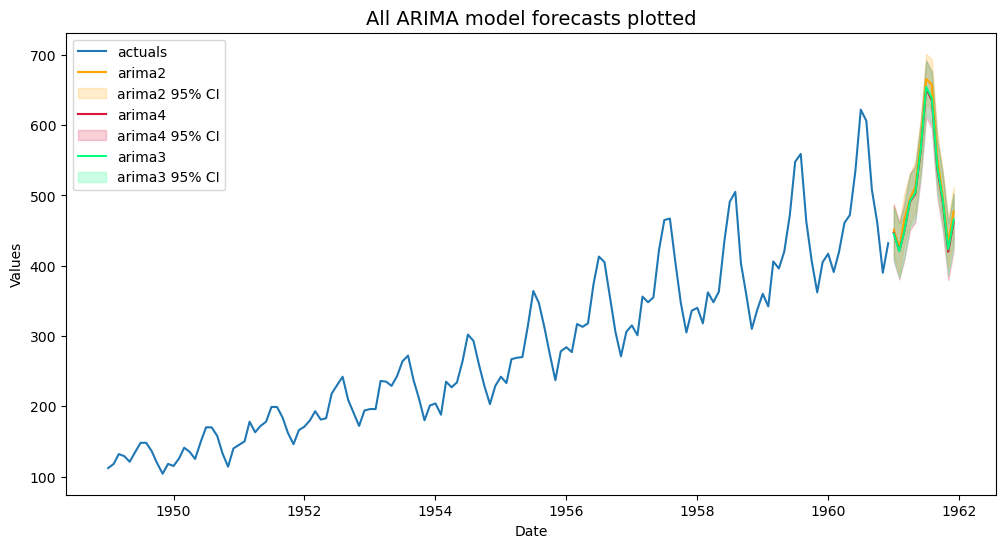
f.plot(ci=True,models=['arima2','arima3','arima4'],order_by='TestSetMAPE')
plt.title('All ARIMA model forecasts plotted',size=14)
plt.show()
../_images/arima_arima_27_0.png 
[ ]: