LinkedIn Silverkite
Silverkite is a model from the greykite package, developed by LinkedIn. It is considered an automated modeling procedure, like Facebook Prophet. It has its own database of holidays it forecasts with and attempts to tune its parameters automatically. The model itself is a type of linear regression with changepoints and regularization.
In this notebook, the following concepts are covered:
1. Loading Forecaster objects with external regressors
2. Forecasting with default silverkite model
3. Modifying changepoints in silverkite model
4. Tuning silverkite model
5. Forecasting on differenced data
6. Model summaries
install greykite:
pip install greykiteread more about grekite: https://engineering.linkedin.com/blog/2021/greykite–a-flexible–intuitive–and-fast-forecasting-library
see the combo notebook for an overview of this dataset with EDA
[1]:
import pandas as pd
import pandas_datareader as pdr
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from dateutil.relativedelta import relativedelta
from scalecast.Forecaster import Forecaster
from scalecast.util import find_optimal_transformation
from scalecast.Pipeline import Pipeline
[2]:
df = pdr.get_data_fred(['HOUSTNSA','JHDUSRGDPBR'],start='1900-01-01',end='2021-12-31')
df['JHDUSRGDPBR'] = df['JHDUSRGDPBR'].fillna(method='ffill').fillna(0)
f = Forecaster(y=df['HOUSTNSA'],current_dates=df.index)
f
[2]:
Forecaster(
DateStartActuals=1959-01-01T00:00:00.000000000
DateEndActuals=2021-12-01T00:00:00.000000000
Freq=MS
N_actuals=756
ForecastLength=0
Xvars=[]
TestLength=0
ValidationMetric=rmse
ForecastsEvaluated=[]
CILevel=None
CurrentEstimator=mlr
GridsFile=Grids
)
Prepare Forecast
Prepare the Recession Indicator
use as an exogenous regressor
[3]:
# prepare recession indicator for future
# assume no future recessions in next two years
recessions = df.reset_index()[['DATE','JHDUSRGDPBR']]
fut_recessions = pd.DataFrame({
'DATE':pd.date_range(
start=recessions['DATE'].max(),
periods=25,
freq='MS'
).values[1:],
'JHDUSRGDPBR':[0]*24}
)
recessions = pd.concat([recessions,fut_recessions])
recessions.tail()
[3]:
| DATE | JHDUSRGDPBR | |
|---|---|---|
| 19 | 2023-08-01 | 0.0 |
| 20 | 2023-09-01 | 0.0 |
| 21 | 2023-10-01 | 0.0 |
| 22 | 2023-11-01 | 0.0 |
| 23 | 2023-12-01 | 0.0 |
Load Object with Parameters and Regressors
Forecast length: 24 periods (two years)
Test length: 24 periods
External recession indicator
Conformal confidence intervals
[4]:
f.generate_future_dates(24)
f.set_test_length(24)
f.ingest_Xvars_df(recessions,date_col="DATE") # let the model consider recesssions
f.add_ar_terms(range(24,37)) # we can use direct autoregressive forecasting with silverkite
f.eval_cis()
f
[4]:
Forecaster(
DateStartActuals=1959-01-01T00:00:00.000000000
DateEndActuals=2021-12-01T00:00:00.000000000
Freq=MS
N_actuals=756
ForecastLength=24
Xvars=['JHDUSRGDPBR', 'AR24', 'AR25', 'AR26', 'AR27', 'AR28', 'AR29', 'AR30', 'AR31', 'AR32', 'AR33', 'AR34', 'AR35', 'AR36']
TestLength=24
ValidationMetric=rmse
ForecastsEvaluated=[]
CILevel=0.95
CurrentEstimator=mlr
GridsFile=Grids
)
Find the optimal set of transformations
[5]:
transformer, reverter = find_optimal_transformation(
f,
estimator='silverkite',
Xvars = 'all',
verbose=True,
)
Using silverkite model to find the best transformation set on 1 test sets, each 24 in length.
Last transformer tried:
[]
Score (rmse): 25.001200396713674
--------------------------------------------------
Last transformer tried:
[('DetrendTransform', {'loess': True})]
Score (rmse): 49.79434396750028
--------------------------------------------------
Last transformer tried:
[('DetrendTransform', {'poly_order': 1})]
Score (rmse): 29.65330614730279
--------------------------------------------------
Last transformer tried:
[('DetrendTransform', {'poly_order': 2})]
Score (rmse): 51.360030782675594
--------------------------------------------------
Last transformer tried:
[('DeseasonTransform', {'m': 12, 'model': 'add'})]
Score (rmse): 27.629940902996385
--------------------------------------------------
Last transformer tried:
[('Transform', <function find_optimal_transformation.<locals>.boxcox_tr at 0x7fc8f5ba7670>, {'lmbda': -0.5})]
Score (rmse): 34.23912395743547
--------------------------------------------------
Last transformer tried:
[('Transform', <function find_optimal_transformation.<locals>.boxcox_tr at 0x7fc8f5ba7670>, {'lmbda': 0})]
Score (rmse): 30.86898988573646
--------------------------------------------------
Last transformer tried:
[('Transform', <function find_optimal_transformation.<locals>.boxcox_tr at 0x7fc8f5ba7670>, {'lmbda': 0.5})]
Score (rmse): 27.770186050360685
--------------------------------------------------
Last transformer tried:
[('DiffTransform', 1)]
Score (rmse): 27.461269567182537
--------------------------------------------------
Last transformer tried:
[('DiffTransform', 12)]
Score (rmse): 24.20622290670972
--------------------------------------------------
Last transformer tried:
[('DiffTransform', 12), ('ScaleTransform',)]
Score (rmse): 24.20622290670972
--------------------------------------------------
Last transformer tried:
[('DiffTransform', 12), ('MinMaxTransform',)]
Score (rmse): 24.20622290670973
--------------------------------------------------
Last transformer tried:
[('DiffTransform', 12), ('RobustScaleTransform',)]
Score (rmse): 24.20622290670972
--------------------------------------------------
Final Selection:
[('DiffTransform', 12)]
One seasonal difference chosen.
Apply the silverkite model
[6]:
silverkite_grid = {
'changepoints':[2,None],
'Xvars':[None,'all']
}
[7]:
def forecaster(f):
f.set_estimator('silverkite')
f.ingest_grid(silverkite_grid)
f.cross_validate(
k=3,
verbose=True,
test_length=24,
)
f.auto_forecast()
matplotlib.use("nbAgg")
%matplotlib inline
[8]:
pipeline = Pipeline(
steps = [
('Transform',transformer),
('Forecast',forecaster),
('Revert',reverter),
]
)
[9]:
f = pipeline.fit_predict(f)
Num hyperparams to try for the silverkite model: 4.
Fold 0: Train size: 696 (1960-01-01 00:00:00 - 2017-12-01 00:00:00). Test Size: 24 (2018-01-01 00:00:00 - 2019-12-01 00:00:00).
Fold 1: Train size: 672 (1960-01-01 00:00:00 - 2015-12-01 00:00:00). Test Size: 24 (2016-01-01 00:00:00 - 2017-12-01 00:00:00).
Fold 2: Train size: 648 (1960-01-01 00:00:00 - 2013-12-01 00:00:00). Test Size: 24 (2014-01-01 00:00:00 - 2015-12-01 00:00:00).
Chosen paramaters: {'changepoints': 2, 'Xvars': None}.
Now we can see the results plotted.
[10]:
f.plot_test_set(ci=True)
plt.show()
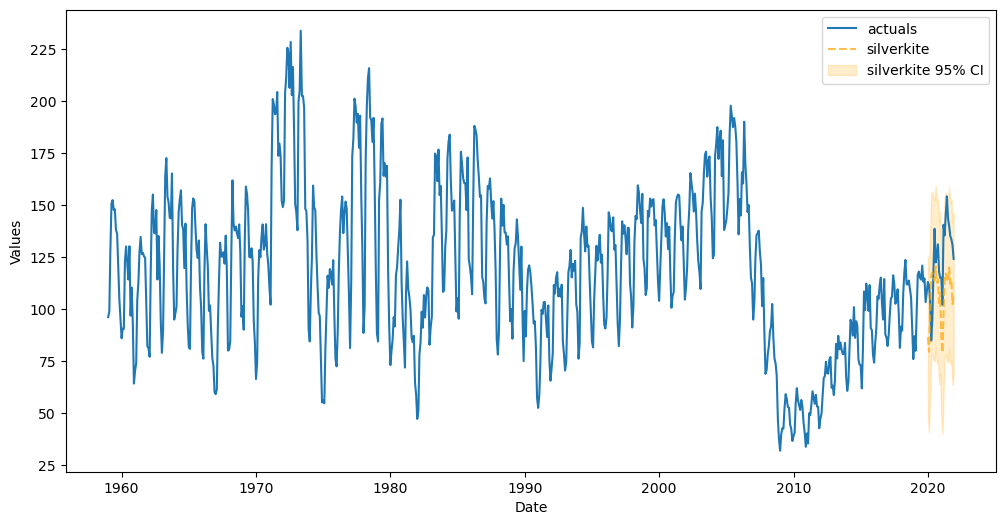
[11]:
f.plot(ci=True)
plt.show()
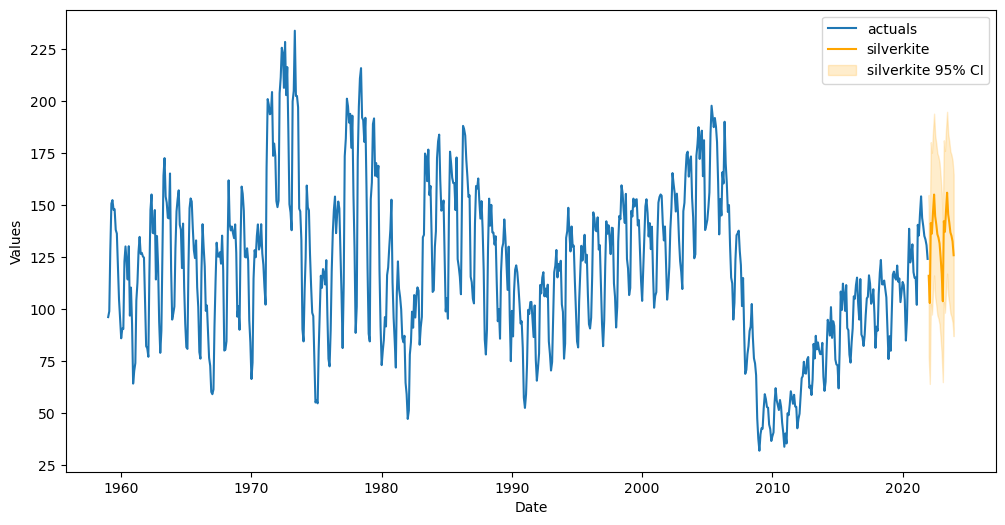
Scalecast model summary:
[12]:
f.export('model_summaries')
[12]:
| ModelNickname | Estimator | Xvars | HyperParams | Observations | DynamicallyTested | TestSetLength | CILevel | ValidationMetric | ValidationMetricValue | ... | weights | best_model | InSampleRMSE | InSampleMAPE | InSampleMAE | InSampleR2 | TestSetRMSE | TestSetMAPE | TestSetMAE | TestSetR2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | silverkite | silverkite | [] | {'changepoints': 2} | 744 | True | 24 | 0.95 | rmse | 11.124548 | ... | NaN | True | 35.682039 | 0.292353 | 27.853908 | 0.124307 | 24.206223 | 0.177581 | 21.884643 | -1.097076 |
1 rows × 21 columns
Greykite model summary:
[13]:
f.save_summary_stats()
f.export_summary_stats('silverkite')
[13]:
| Estimate | Std. Err | Pr(>)_boot | sig. code | 95%CI | |
|---|---|---|---|---|---|
| Pred_col | |||||
| Intercept | -0.627656 | 1.621083 | 0.702 | [-3.8531285086971647, 2.356499683299088] | |
| C(Q('events_Chinese New Year'), levels=['', 'event'])[T.event] | 0.000442 | 0.000428 | 0.300 | [-0.0002607304049092221, 0.0013420810713082817] | |
| C(Q('events_Chinese New Year_minus_1'), levels=['', 'event'])[T.event] | 0.000344 | 0.000542 | 0.534 | [-0.0006032882997487039, 0.001518463518762043] | |
| C(Q('events_Chinese New Year_minus_2'), levels=['', 'event'])[T.event] | -0.000170 | 0.000442 | 0.698 | [-0.0009151696081354368, 0.0007430782634949848] | |
| C(Q('events_Chinese New Year_plus_1'), levels=['', 'event'])[T.event] | 0.000464 | 0.000415 | 0.268 | [-0.0001755691414453123, 0.0013656991823609355] | |
| C(Q('events_Chinese New Year_plus_2'), levels=['', 'event'])[T.event] | -0.000005 | 0.000319 | 0.988 | [-0.0005955917978176905, 0.0006458427330378518] | |
| C(Q('events_Christmas Day'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Christmas Day_minus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Christmas Day_minus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Christmas Day_plus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Christmas Day_plus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Good Friday'), levels=['', 'event'])[T.event] | 0.000652 | 0.000523 | 0.200 | [-0.00011973412921468802, 0.0017832190805516328] | |
| C(Q('events_Good Friday_minus_1'), levels=['', 'event'])[T.event] | 0.000681 | 0.000538 | 0.248 | [-6.180472787720763e-06, 0.0019063632891964072] | |
| C(Q('events_Good Friday_minus_2'), levels=['', 'event'])[T.event] | 0.000129 | 0.000125 | 0.162 | [0.0, 0.00041798826584095656] | |
| C(Q('events_Good Friday_plus_1'), levels=['', 'event'])[T.event] | 0.000012 | 0.000141 | 0.956 | [-0.00025339241691280985, 0.0003210267888415958] | |
| C(Q('events_Good Friday_plus_2'), levels=['', 'event'])[T.event] | 0.000115 | 0.000117 | 0.536 | [0.0, 0.00037724309283902117] | |
| C(Q('events_Independence Day'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Independence Day_minus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Independence Day_minus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Independence Day_plus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Independence Day_plus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Labor Day'), levels=['', 'event'])[T.event] | -0.000107 | 0.002290 | 0.966 | [-0.004791044889046614, 0.004335130028251806] | |
| C(Q('events_Labor Day_minus_1'), levels=['', 'event'])[T.event] | 0.000182 | 0.000642 | 0.768 | [-0.001172023060659738, 0.0013385029209143616] | |
| C(Q('events_Labor Day_minus_2'), levels=['', 'event'])[T.event] | -0.001285 | 0.000824 | 0.108 | [-0.0031060576549147042, 0.00012062622545997192] | |
| C(Q('events_Labor Day_plus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Labor Day_plus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Memorial Day'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Memorial Day_minus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Memorial Day_minus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Memorial Day_plus_1'), levels=['', 'event'])[T.event] | 0.001146 | 0.000853 | 0.178 | [-0.00023374375090142146, 0.002951211730207247] | |
| C(Q('events_Memorial Day_plus_2'), levels=['', 'event'])[T.event] | 0.001383 | 0.000981 | 0.152 | [-0.0003991890982334486, 0.0033048549227503946] | |
| C(Q('events_New Years Day'), levels=['', 'event'])[T.event] | 0.000124 | 0.001557 | 0.934 | [-0.002761111121212117, 0.003332850157173629] | |
| C(Q('events_New Years Day_minus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_New Years Day_minus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_New Years Day_plus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_New Years Day_plus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Other'), levels=['', 'event'])[T.event] | 0.001696 | 0.003285 | 0.616 | [-0.0047755062438510675, 0.007800442595334815] | |
| C(Q('events_Other_minus_1'), levels=['', 'event'])[T.event] | 0.003931 | 0.003047 | 0.190 | [-0.0019763326484872395, 0.009885947626548024] | |
| C(Q('events_Other_minus_2'), levels=['', 'event'])[T.event] | 0.001698 | 0.002451 | 0.486 | [-0.003617400314516922, 0.006242402118271505] | |
| C(Q('events_Other_plus_1'), levels=['', 'event'])[T.event] | 0.001474 | 0.002845 | 0.594 | [-0.004060351507498453, 0.006938519402375477] | |
| C(Q('events_Other_plus_2'), levels=['', 'event'])[T.event] | 0.000897 | 0.002365 | 0.682 | [-0.0039291870020548856, 0.005265469190849324] | |
| C(Q('events_Thanksgiving'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Thanksgiving_minus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Thanksgiving_minus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Thanksgiving_plus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Thanksgiving_plus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Veterans Day'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Veterans Day_minus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Veterans Day_minus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Veterans Day_plus_1'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| C(Q('events_Veterans Day_plus_2'), levels=['', 'event'])[T.event] | 0.000000 | 0.000000 | 1.000 | [0.0, 0.0] | |
| ct1 | 0.023843 | 0.033266 | 0.470 | [-0.037338129675015985, 0.09046991435719089] |
[ ]: