Scikit-Learn Models

This notebook showcases the scalecast wrapper around scikit-learn models.

The data is available for download here: https://www.kaggle.com/datasets/bobnau/daily-website-visitors
See the blog post: https://medium.com/towards-data-science/expand-your-time-series-arsenal-with-these-models-10c807d37558
[1]:

import pandas as pd
import numpy as np
import pandas_datareader as pdr
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from dateutil.relativedelta import relativedelta
from scalecast.Forecaster import Forecaster
from scalecast import GridGenerator
from scalecast.auxmodels import mlp_stack
from tqdm.notebook import tqdm
from sklearn.ensemble import BaggingRegressor
from sklearn.ensemble import StackingRegressor
from sklearn.neural_network import MLPRegressor

pd.set_option('max_colwidth',500)
pd.set_option('display.max_rows',500)

[2]:

def plot_test_export_summaries(f):
    """ exports the relevant statisitcal information and displays a plot of the test-set results for the last model run
    """
    f.plot_test_set(models=f.estimator,ci=True)
    plt.title(f'{f.estimator} test-set results',size=16)
    plt.show()
    return f.export('model_summaries',determine_best_by='TestSetMAPE')[
        [
            'ModelNickname',
            'HyperParams',
            'TestSetMAPE',
            'TestSetR2',
            'InSampleMAPE',
            'InSampleR2'
        ]
    ]

We will bring in the default grids from scalecast and tune some of our models this way. For others, we will create our own grids.

[3]:

GridGenerator.get_example_grids()

[4]:

data = pd.read_csv('daily-website-visitors.csv')
data.head()

[4]:
Row Day Day.Of.Week Date Page.Loads Unique.Visits First.Time.Visits Returning.Visits
0 1 Sunday 1 9/14/2014 2,146 1,582 1430 152
1 2 Monday 2 9/15/2014 3,621 2,528 2297 231
2 3 Tuesday 3 9/16/2014 3,698 2,630 2352 278
3 4 Wednesday 4 9/17/2014 3,667 2,614 2327 287
4 5 Thursday 5 9/18/2014 3,316 2,366 2130 236 
[5]:

data.shape

[5]:

(2167, 8)

[6]:

f=Forecaster(y=data['First.Time.Visits'],current_dates=data['Date'])
f.plot()
plt.title('Orig Series',size=16)
plt.show()
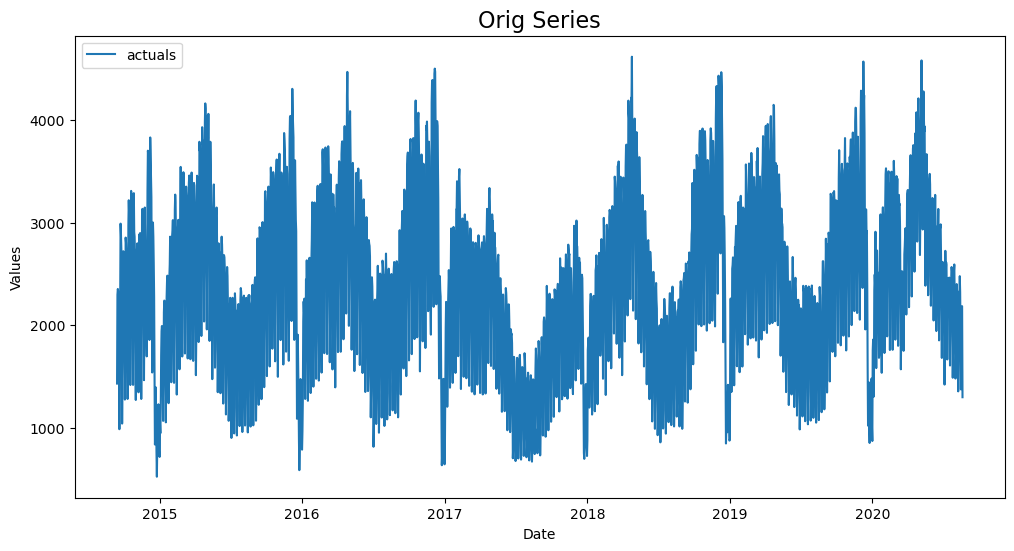
../_images/sklearn_sklearn_7_0.png

Not all models we will showcase come standard in scalecast, but we can easily add them by using the code below:

[7]:

f.add_sklearn_estimator(BaggingRegressor,'bagging')
f.add_sklearn_estimator(StackingRegressor,'stacking')

For more EDA on this dataset, see the prophet example: https://scalecast-examples.readthedocs.io/en/latest/prophet/prophet.html#EDA

Prepare Forecast

  • 60-day forecast horizon

  • 20% test split

  • Turn confidence intervals on

  • Add time series regressors:

  • 7 autoregressive terms

  • 4 seasonal autoregressive terms spaced 7-periods apart

  • month, quarter, week, and day of year with a fournier transformation

  • dayofweek, leap year, and week as dummy variables

  • year

[8]:

fcst_length = 60
f.generate_future_dates(fcst_length)
f.set_test_length(.2)
f.eval_cis() # tell the object to build confidence intervals for all models
f.add_ar_terms(7)
f.add_AR_terms((4,7))
f.add_seasonal_regressors('month','quarter','week','dayofyear',raw=False,sincos=True)
f.add_seasonal_regressors('dayofweek','is_leap_year','week',raw=False,dummy=True,drop_first=True)
f.add_seasonal_regressors('year')
f

[8]:

Forecaster(
    DateStartActuals=2014-09-14T00:00:00.000000000
    DateEndActuals=2020-08-19T00:00:00.000000000
    Freq=D
    N_actuals=2167
    ForecastLength=60
    Xvars=['AR1', 'AR2', 'AR3', 'AR4', 'AR5', 'AR6', 'AR7', 'AR14', 'AR21', 'AR28', 'monthsin', 'monthcos', 'quartersin', 'quartercos', 'weeksin', 'weekcos', 'dayofyearsin', 'dayofyearcos', 'dayofweek_1', 'dayofweek_2', 'dayofweek_3', 'dayofweek_4', 'dayofweek_5', 'dayofweek_6', 'is_leap_year_True', 'week_10', 'week_11', 'week_12', 'week_13', 'week_14', 'week_15', 'week_16', 'week_17', 'week_18', 'week_19', 'week_2', 'week_20', 'week_21', 'week_22', 'week_23', 'week_24', 'week_25', 'week_26', 'week_27', 'week_28', 'week_29', 'week_3', 'week_30', 'week_31', 'week_32', 'week_33', 'week_34', 'week_35', 'week_36', 'week_37', 'week_38', 'week_39', 'week_4', 'week_40', 'week_41', 'week_42', 'week_43', 'week_44', 'week_45', 'week_46', 'week_47', 'week_48', 'week_49', 'week_5', 'week_50', 'week_51', 'week_52', 'week_53', 'week_6', 'week_7', 'week_8', 'week_9', 'year']
    TestLength=433
    ValidationMetric=rmse
    ForecastsEvaluated=[]
    CILevel=0.95
    CurrentEstimator=mlr
    GridsFile=Grids
)

MLR

  • use default parameters (which means all input vars are scaled with a minmax scaler by default for all sklearn models)

[9]:

f.set_estimator('mlr')
f.manual_forecast()

[10]:

plot_test_export_summaries(f)
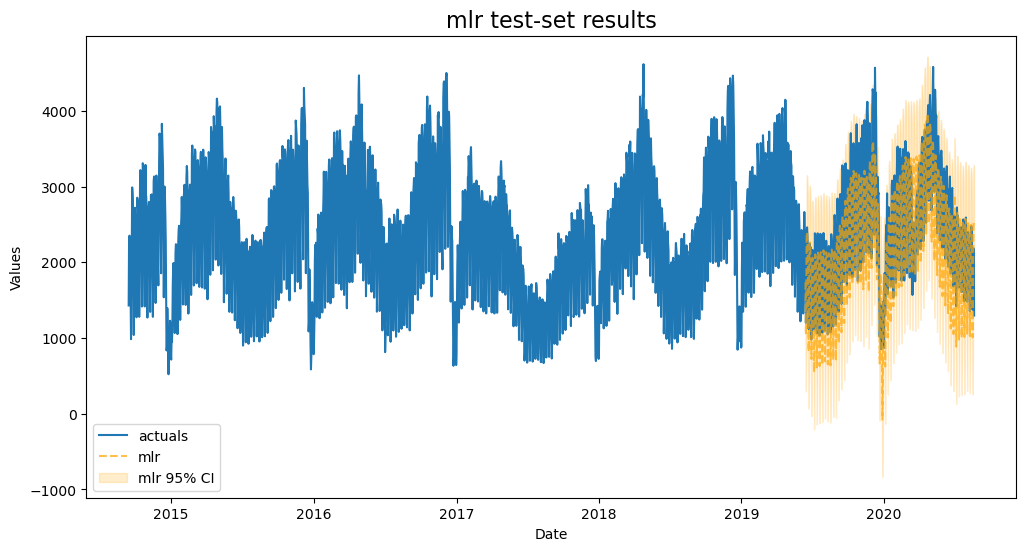
../_images/sklearn_sklearn_15_0.png 
[10]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 mlr {} 0.14485 0.733553 0.064183 0.953482

Lasso

  • tune alpha with 100 choices using 3-fold cross validation

[11]:

f.set_estimator('lasso')
lasso_grid = {'alpha':np.linspace(0,2,100)}
f.ingest_grid(lasso_grid)
f.cross_validate(k=3)
f.auto_forecast()

[12]:

plot_test_export_summaries(f)
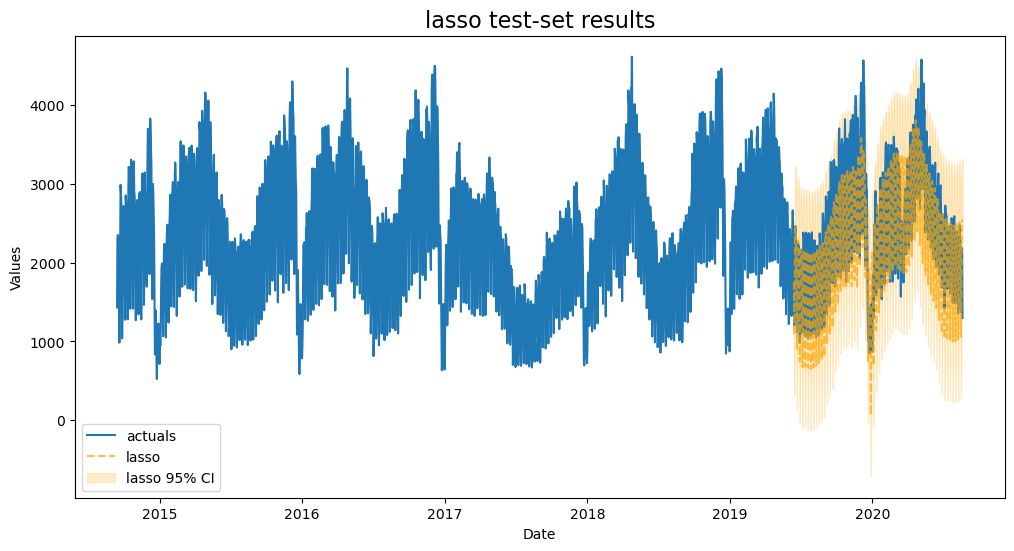
../_images/sklearn_sklearn_18_0.png 
[12]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
1 mlr {} 0.144850 0.733553 0.064183 0.953482

Ridge

  • tune alpha with the same grid used for lasso

[13]:

f.set_estimator('ridge')
f.ingest_grid(lasso_grid)
f.cross_validate(k=3)
f.auto_forecast()

[14]:

plot_test_export_summaries(f)
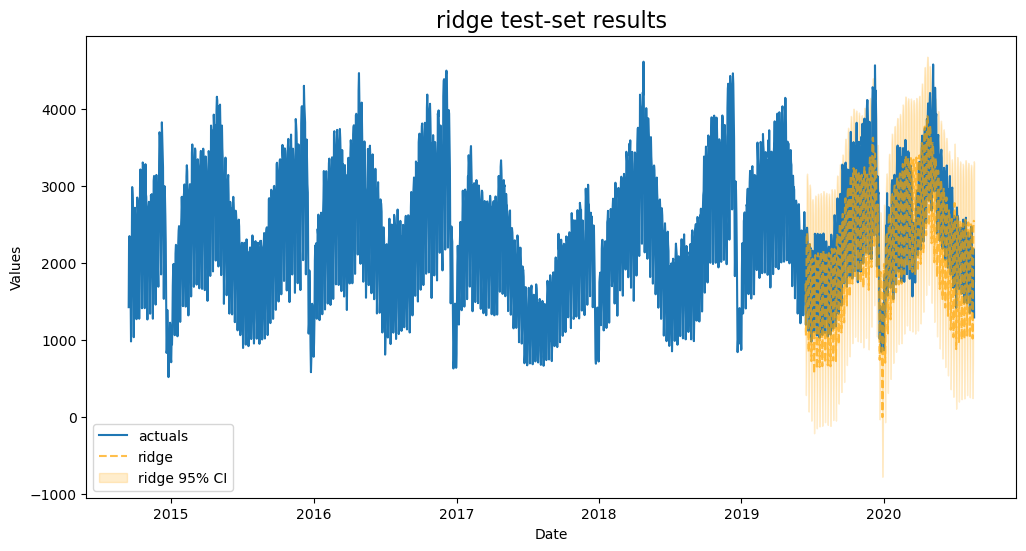
../_images/sklearn_sklearn_21_0.png 
[14]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
1 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
2 mlr {} 0.144850 0.733553 0.064183 0.953482

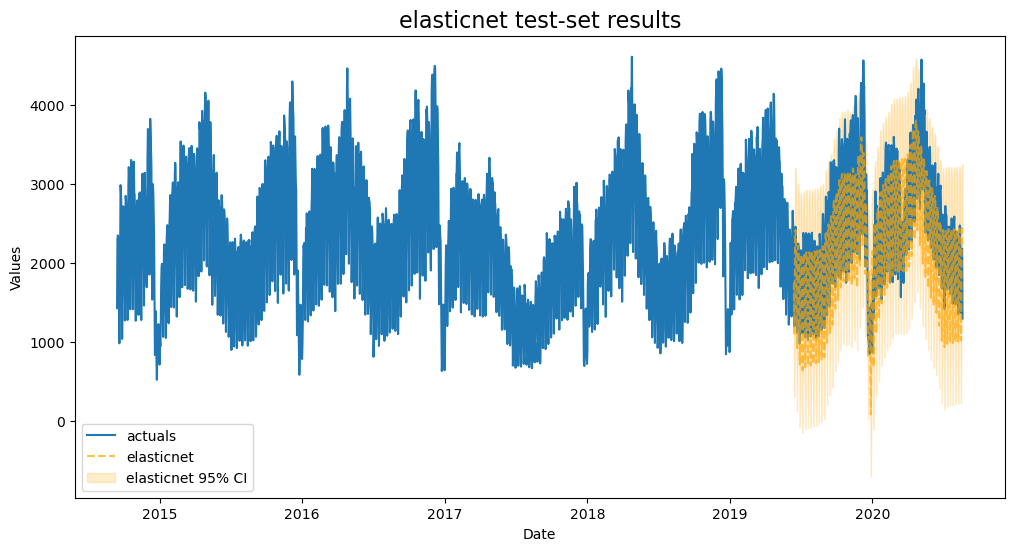
Elasticnet

  • this model mixes L1 and L2 regularization parameters

  • its default grid is pretty good for finding the optimal alpha value and l1 ratio

[15]:

f.set_estimator('elasticnet')
f.cross_validate(k=3)
f.auto_forecast()

[16]:

plot_test_export_summaries(f)
../_images/sklearn_sklearn_24_0.png 
[16]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
1 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
2 elasticnet {'alpha': 2.0, 'l1_ratio': 1, 'normalizer': 'scale'} 0.141774 0.733125 0.065364 0.952024
3 mlr {} 0.144850 0.733553 0.064183 0.953482

RF

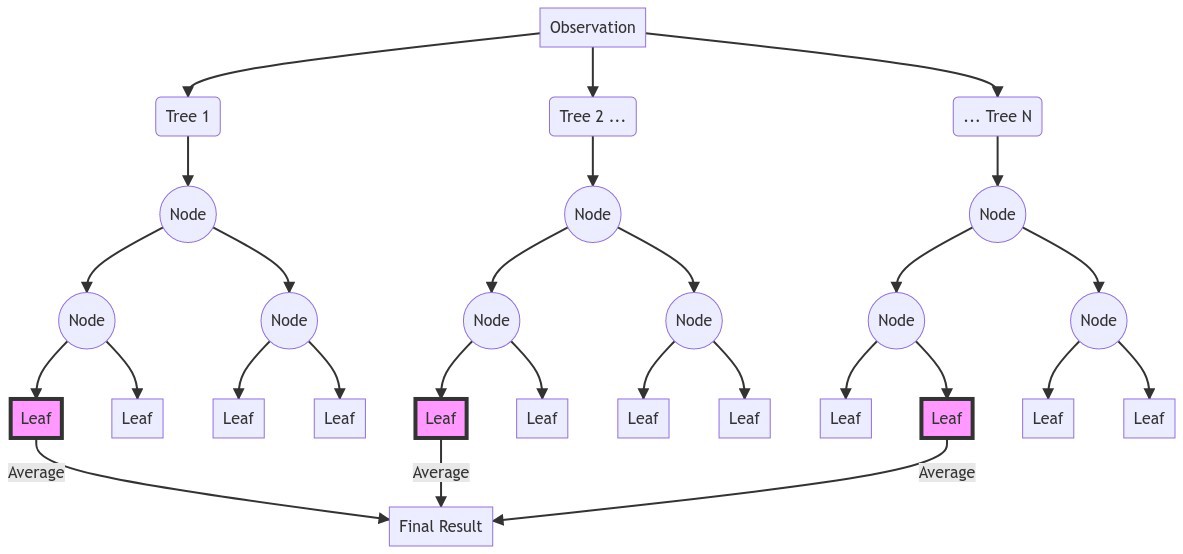
Random Forest

create a grid to tune Random Forest with more options than what is available in the default grids

[17]:

f.set_estimator('rf')
rf_grid = {
    'max_depth':[2,3,4,5],
    'n_estimators':[100,200,500],
    'max_features':['auto','sqrt','log2'],
    'max_samples':[.75,.9,1],
}
f.ingest_grid(rf_grid)
f.cross_validate(k=3)
f.auto_forecast()

[18]:

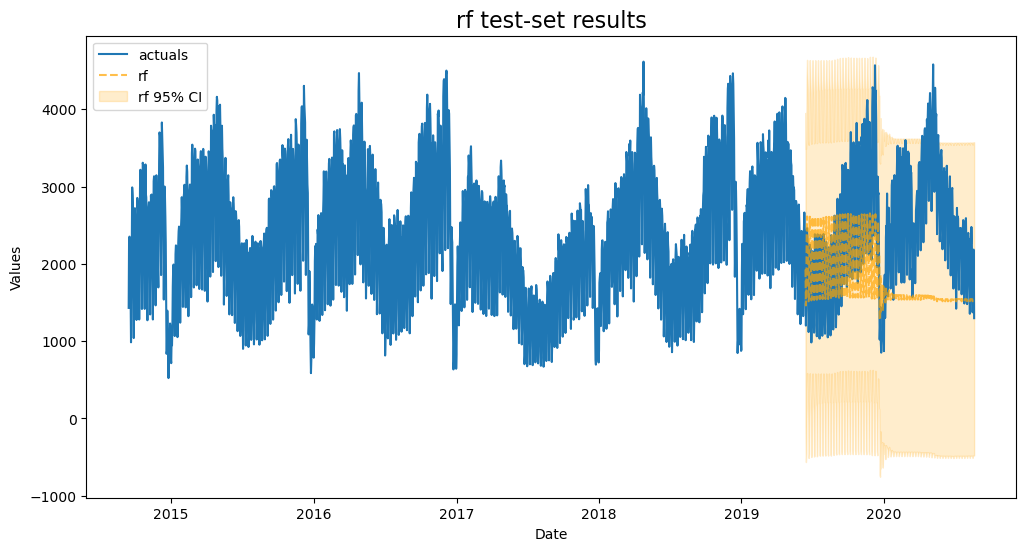
plot_test_export_summaries(f)
../_images/sklearn_sklearn_28_0.png 
[18]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
1 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
2 mlr {} 0.144850 0.733553 0.064183 0.953482
3 elasticnet {'alpha': 2.0, 'l1_ratio': 0, 'normalizer': None} 0.259322 0.152033 0.092402 0.904719
4 rf {'max_depth': 5, 'n_estimators': 200, 'max_features': 'auto', 'max_samples': 0.75} 0.318096 -0.916329 0.083374 0.918095

So far, both using a visual inspection and examing its test-set performance, Random Forest does worse than all others.

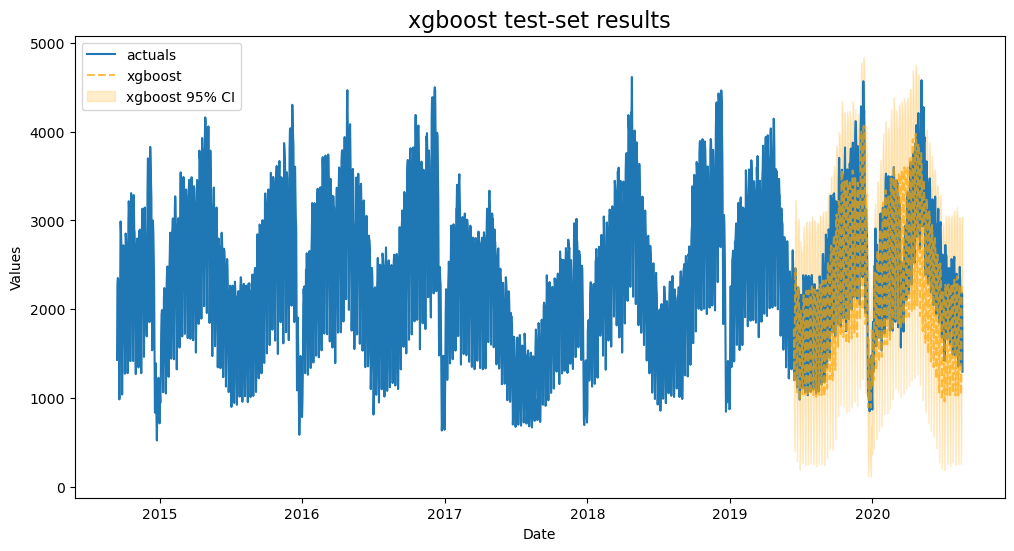
XGBoost

  • Build a grid to tune XGBoost

[19]:

f.set_estimator('xgboost')
xgboost_grid = {
     'n_estimators':[150,200,250],
     'scale_pos_weight':[5,10],
     'learning_rate':[0.1,0.2],
     'gamma':[0,3,5],
     'subsample':[0.8,0.9]
}
f.ingest_grid(xgboost_grid)
f.cross_validate(k=3)
f.auto_forecast()

[20]:

plot_test_export_summaries(f)
../_images/sklearn_sklearn_32_0.png 
[20]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 xgboost {'n_estimators': 150, 'scale_pos_weight': 5, 'learning_rate': 0.1, 'gamma': 5, 'subsample': 0.9} 0.115551 0.769377 0.018676 0.995667
1 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
2 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
3 mlr {} 0.144850 0.733553 0.064183 0.953482
4 elasticnet {'alpha': 2.0, 'l1_ratio': 0, 'normalizer': None} 0.259322 0.152033 0.092402 0.904719
5 rf {'max_depth': 5, 'n_estimators': 200, 'max_features': 'auto', 'max_samples': 0.75} 0.318096 -0.916329 0.083374 0.918095

This is our best model so far using the test MAPE as the metric to determine that by. It appears to be also be highly overfit.

LightGBM

  • Build a grid to tune LightGBM

[21]:

f.set_estimator('lightgbm')
lightgbm_grid = {
    'n_estimators':[150,200,250],
    'boosting_type':['gbdt','dart','goss'],
    'max_depth':[1,2,3],
    'learning_rate':[0.001,0.01,0.1],
    'reg_alpha':np.linspace(0,1,5),
    'reg_lambda':np.linspace(0,1,5),
    'num_leaves':np.arange(5,50,5),
}
f.ingest_grid(lightgbm_grid)
f.limit_grid_size(100,random_seed=2)
f.cross_validate(k=3)
f.auto_forecast()

[22]:

plot_test_export_summaries(f)
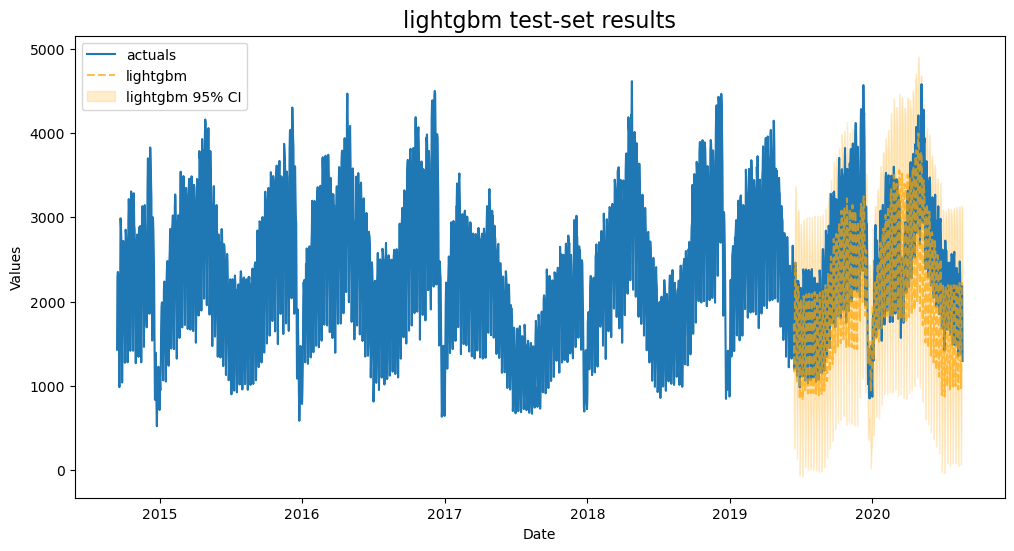
../_images/sklearn_sklearn_36_0.png 
[22]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 xgboost {'n_estimators': 150, 'scale_pos_weight': 5, 'learning_rate': 0.1, 'gamma': 5, 'subsample': 0.9} 0.115551 0.769377 0.018676 0.995667
1 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
2 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
3 mlr {} 0.144850 0.733553 0.064183 0.953482
4 lightgbm {'n_estimators': 200, 'boosting_type': 'goss', 'max_depth': 3, 'learning_rate': 0.1, 'reg_alpha': 0.25, 'reg_lambda': 1.0, 'num_leaves': 35} 0.166747 0.592318 0.050726 0.970159
5 elasticnet {'alpha': 2.0, 'l1_ratio': 0, 'normalizer': None} 0.259322 0.152033 0.092402 0.904719
6 rf {'max_depth': 5, 'n_estimators': 200, 'max_features': 'auto', 'max_samples': 0.75} 0.318096 -0.916329 0.083374 0.918095

SGD

  • Use the default Stochastic Gradient Descent grid

[23]:

f.set_estimator('sgd')
f.cross_validate(k=3)
f.auto_forecast()

Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations

[24]:

plot_test_export_summaries(f)
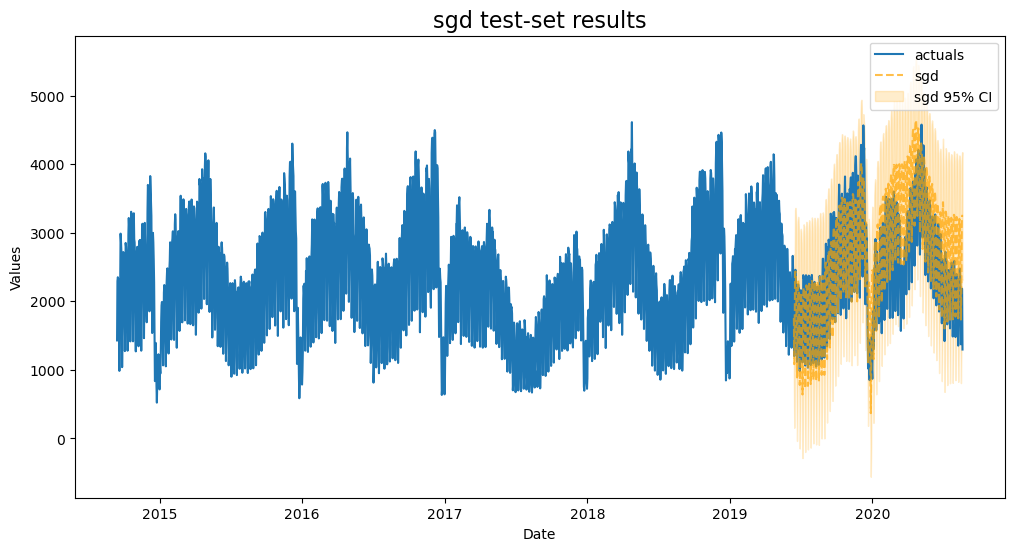
../_images/sklearn_sklearn_39_0.png 
[24]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 xgboost {'n_estimators': 150, 'scale_pos_weight': 5, 'learning_rate': 0.1, 'gamma': 5, 'subsample': 0.9} 0.115551 0.769377 0.018676 0.995667
1 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
2 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
3 mlr {} 0.144850 0.733553 0.064183 0.953482
4 sgd {'penalty': 'elasticnet', 'l1_ratio': 1, 'learning_rate': 'constant'} 0.166129 0.609554 0.065153 0.951795
5 lightgbm {'n_estimators': 200, 'boosting_type': 'goss', 'max_depth': 3, 'learning_rate': 0.1, 'reg_alpha': 0.25, 'reg_lambda': 1.0, 'num_leaves': 35} 0.166747 0.592318 0.050726 0.970159
6 elasticnet {'alpha': 2.0, 'l1_ratio': 0, 'normalizer': None} 0.259322 0.152033 0.092402 0.904719
7 rf {'max_depth': 5, 'n_estimators': 200, 'max_features': 'auto', 'max_samples': 0.75} 0.318096 -0.916329 0.083374 0.918095

KNN

  • Use the default K-nearest Neighbors grid

[25]:

f.set_estimator('knn')
f.cross_validate(k=3)
f.auto_forecast()

Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations
Finished loading model, total used 200 iterations

[26]:

plot_test_export_summaries(f)
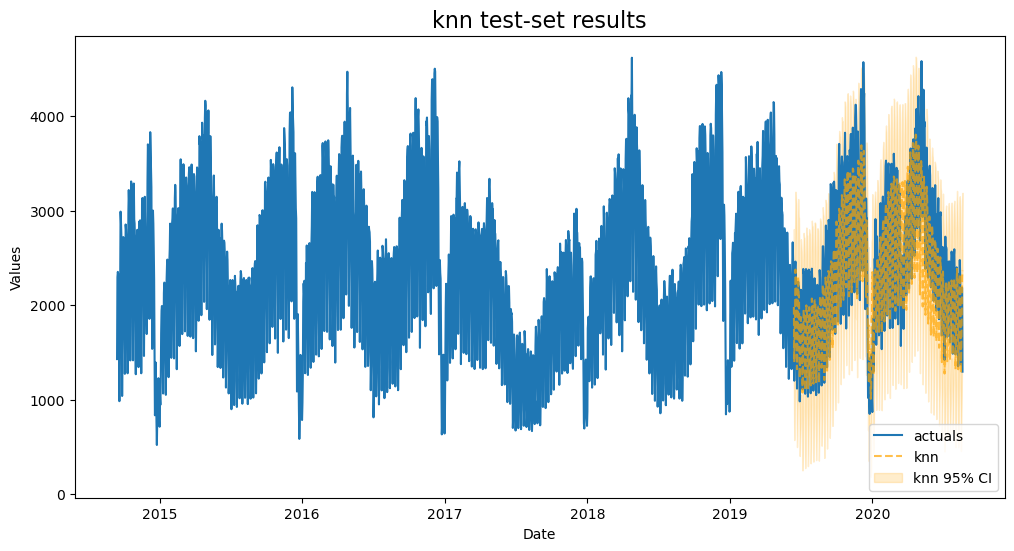
../_images/sklearn_sklearn_42_0.png 
[26]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 xgboost {'n_estimators': 150, 'scale_pos_weight': 5, 'learning_rate': 0.1, 'gamma': 5, 'subsample': 0.9} 0.115551 0.769377 0.018676 0.995667
1 knn {'n_neighbors': 20, 'weights': 'uniform'} 0.130121 0.713268 0.117198 0.873220
2 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
3 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
4 mlr {} 0.144850 0.733553 0.064183 0.953482
5 sgd {'penalty': 'elasticnet', 'l1_ratio': 1, 'learning_rate': 'constant'} 0.166129 0.609554 0.065153 0.951795
6 lightgbm {'n_estimators': 200, 'boosting_type': 'goss', 'max_depth': 3, 'learning_rate': 0.1, 'reg_alpha': 0.25, 'reg_lambda': 1.0, 'num_leaves': 35} 0.166747 0.592318 0.050726 0.970159
7 elasticnet {'alpha': 2.0, 'l1_ratio': 0, 'normalizer': None} 0.259322 0.152033 0.092402 0.904719
8 rf {'max_depth': 5, 'n_estimators': 200, 'max_features': 'auto', 'max_samples': 0.75} 0.318096 -0.916329 0.083374 0.918095

KNN is our most overfit model so far, but it fits the test-set pretty well.

BaggingRegressor

  • Like Random Forest is a bagging ensemble model using decision trees, we can use a bagging estimator that uses a three-layered mulit-level perceptron to see if the added complexity improves where the Random Forest couldn’t

[28]:

f.set_estimator('bagging')
f.manual_forecast(
    base_estimator = MLPRegressor(
        hidden_layer_sizes=(100,100,100)
        ,solver='lbfgs'
    ),
    max_samples = 0.9,
    max_features = 0.5,
)

Finished loading model, total used 200 iterations

[29]:

plot_test_export_summaries(f)
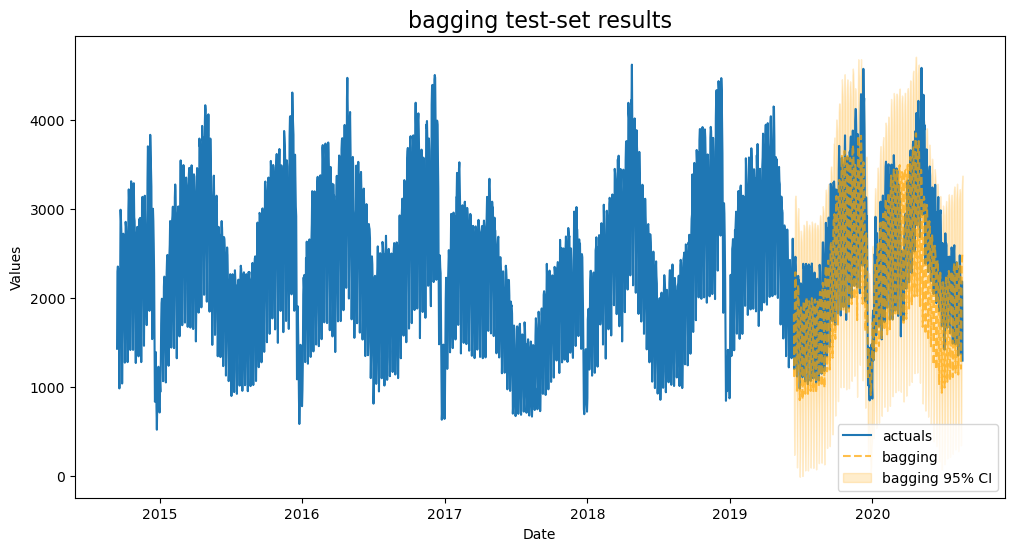
../_images/sklearn_sklearn_46_0.png 
[29]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 xgboost {'n_estimators': 150, 'scale_pos_weight': 5, 'learning_rate': 0.1, 'gamma': 5, 'subsample': 0.9} 0.115551 0.769377 0.018676 0.995667
1 knn {'n_neighbors': 20, 'weights': 'uniform'} 0.130121 0.713268 0.117198 0.873220
2 bagging {'base_estimator': MLPRegressor(hidden_layer_sizes=(100, 100, 100), solver='lbfgs'), 'max_samples': 0.9, 'max_features': 0.5} 0.130137 0.714881 0.050964 0.967984
3 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
4 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
5 mlr {} 0.144850 0.733553 0.064183 0.953482
6 sgd {'penalty': 'elasticnet', 'l1_ratio': 1, 'learning_rate': 'constant'} 0.166129 0.609554 0.065153 0.951795
7 lightgbm {'n_estimators': 200, 'boosting_type': 'goss', 'max_depth': 3, 'learning_rate': 0.1, 'reg_alpha': 0.25, 'reg_lambda': 1.0, 'num_leaves': 35} 0.166747 0.592318 0.050726 0.970159
8 elasticnet {'alpha': 2.0, 'l1_ratio': 0, 'normalizer': None} 0.259322 0.152033 0.092402 0.904719
9 rf {'max_depth': 5, 'n_estimators': 200, 'max_features': 'auto', 'max_samples': 0.75} 0.318096 -0.916329 0.083374 0.918095

This is the best-performing model yet, with less overfitting than XGBoost and KNN.

StackingRegressor

This model will use the predictions of other models as inputs to a “final estimator”. It’s added complexity can mean better performance, although not always.

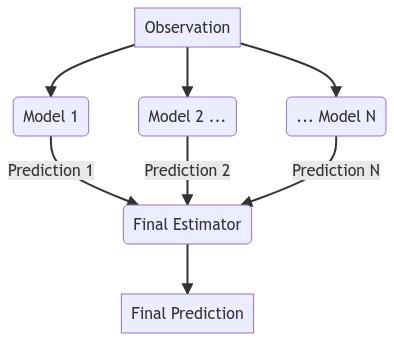
Stacking Regressor

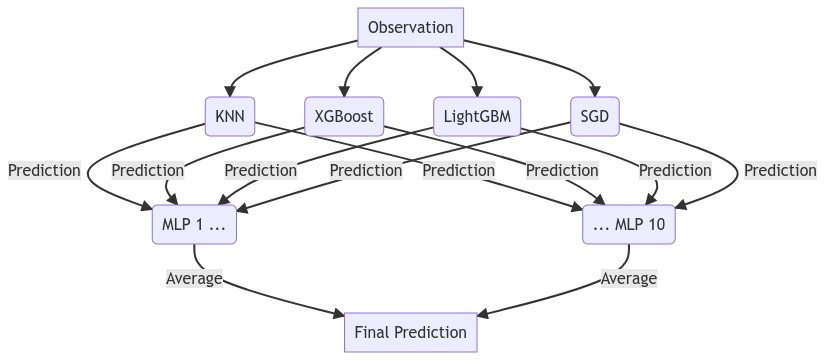
The model that we employ uses the bagged MLP regressor from the previous section as its final estimator, and the tuned knn, xgboost, lightgbm, and sgd models as its inputs.

MLP Stack

[30]:

f.plot_fitted()
plt.title('all models fitted vals',size=16)
plt.show()
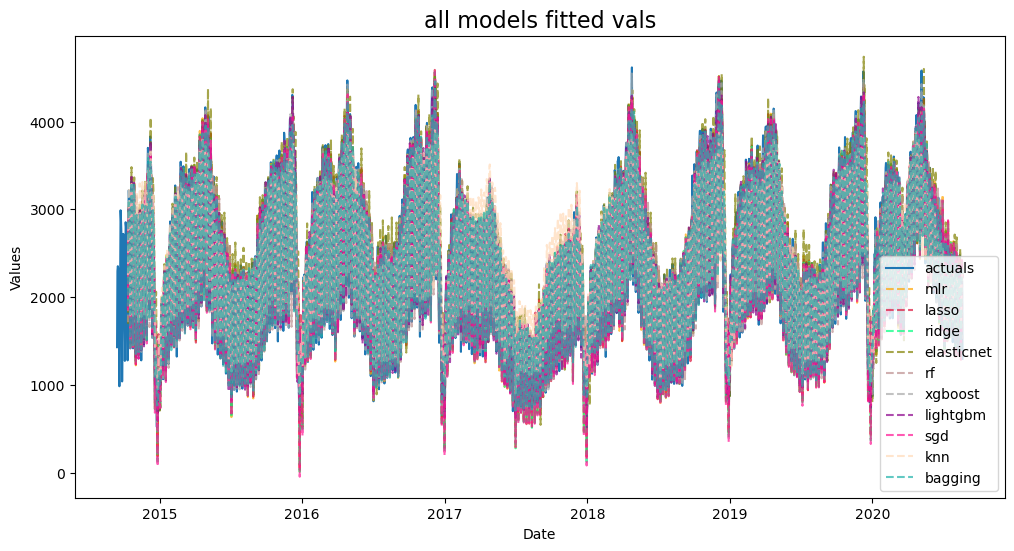
../_images/sklearn_sklearn_49_0.png

Sometimes seeing the fitted values can give a good idea of which models to stack, as you want models that can predict both the highs and lows of the series. However, this graph didn’t tell us much.

We use four of our best performing models to create the model inputs. We use a bagging estimator as the final model.

[31]:

f.set_estimator('stacking')
results = f.export('model_summaries')
estimators = [
    'knn',
    'xgboost',
    'lightgbm',
    'sgd',
]

mlp_stack(f,estimators,call_me='stacking')

Finished loading model, total used 200 iterations

[32]:

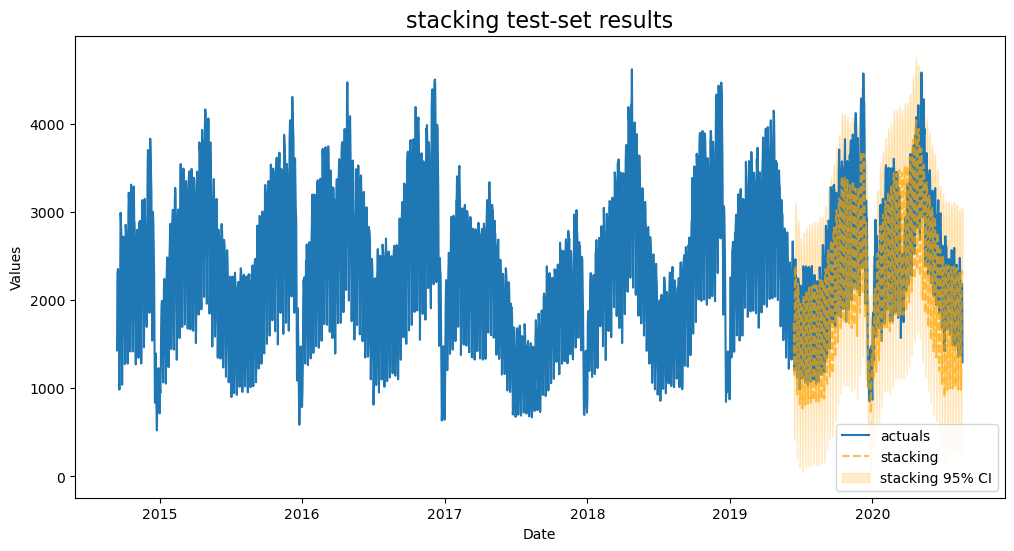
plot_test_export_summaries(f)
../_images/sklearn_sklearn_52_0.png 
[32]:
ModelNickname HyperParams TestSetMAPE TestSetR2 InSampleMAPE InSampleR2
0 xgboost {'n_estimators': 150, 'scale_pos_weight': 5, 'learning_rate': 0.1, 'gamma': 5, 'subsample': 0.9} 0.115551 0.769377 0.018676 0.995667
1 stacking {'estimators': [('knn', KNeighborsRegressor(n_neighbors=20)), ('xgboost', XGBRegressor(base_score=None, booster=None, callbacks=None, colsample_bylevel=None, colsample_bynode=None, colsample_bytree=None, early_stopping_rounds=None, enable_categorical=False, eval_metric=None, feature_types=None, gamma=5, gpu_id=None, grow_policy=None, importance_type=None, interaction_constraints=None, learning_rate=0.1, max_bin=None, ... 0.122353 0.784423 0.040845 0.979992
2 knn {'n_neighbors': 20, 'weights': 'uniform'} 0.130121 0.713268 0.117198 0.873220
3 bagging {'base_estimator': MLPRegressor(hidden_layer_sizes=(100, 100, 100), solver='lbfgs'), 'max_samples': 0.9, 'max_features': 0.5} 0.130137 0.714881 0.050964 0.967984
4 lasso {'alpha': 0.32323232323232326} 0.139526 0.744279 0.065458 0.952205
5 ridge {'alpha': 0.6060606060606061} 0.140560 0.743738 0.064592 0.952812
6 mlr {} 0.144850 0.733553 0.064183 0.953482
7 sgd {'penalty': 'elasticnet', 'l1_ratio': 1, 'learning_rate': 'constant'} 0.166129 0.609554 0.065153 0.951795
8 lightgbm {'n_estimators': 200, 'boosting_type': 'goss', 'max_depth': 3, 'learning_rate': 0.1, 'reg_alpha': 0.25, 'reg_lambda': 1.0, 'num_leaves': 35} 0.166747 0.592318 0.050726 0.970159
9 elasticnet {'alpha': 2.0, 'l1_ratio': 0, 'normalizer': None} 0.259322 0.152033 0.092402 0.904719
10 rf {'max_depth': 5, 'n_estimators': 200, 'max_features': 'auto', 'max_samples': 0.75} 0.318096 -0.916329 0.083374 0.918095

This is our best model with lower amounts of overfitting than some of our other models. We will choose it to make our final forecasts with.

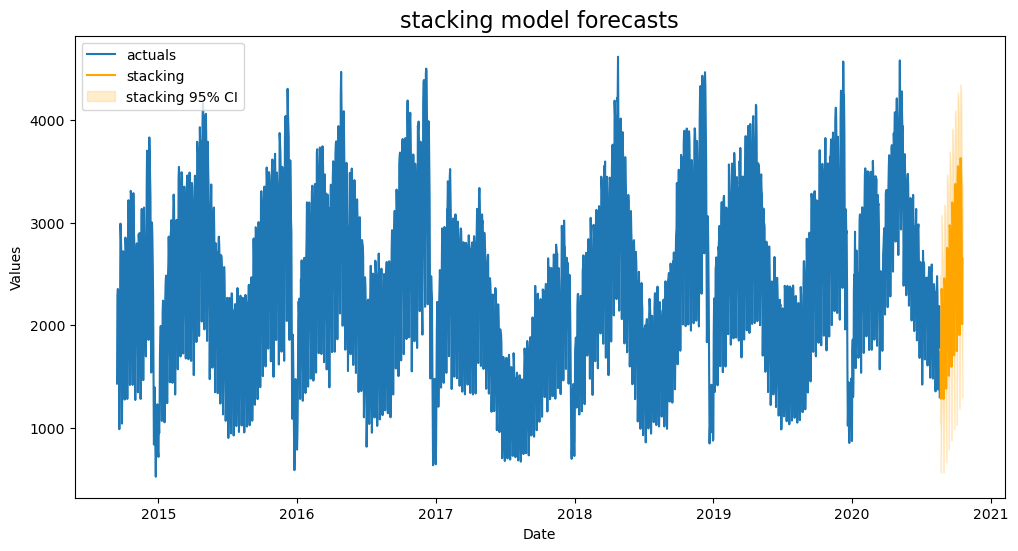
Plot Forecast

[33]:

f.plot('stacking',ci=True)
plt.title('stacking model forecasts',size=16)
plt.show()
../_images/sklearn_sklearn_55_0.png 
[ ]: